Ever wondered how to plan the perfect pizza party? Or maybe you're just trying to figure out how many hotdogs and buns you need so you don't end up with leftovers for a month?
Well, my friends, the secret weapon is the Least Common Multiple (LCM)! And today, we're diving headfirst into the wonderful world of finding the LCM of 25 and 45. Buckle up, buttercup, it's going to be a wild ride!
The Pizza Party Problem (and how LCM saves the day!)
Imagine this: You're hosting a pizza party. You've got 25 of your closest (and hungriest) pals coming over. You're ordering pizzas cut into 25 slices each, but you also have some mini pizzas cut into 45 slices.
You want to make sure everyone gets an equal amount of pizza, and, being the magnificent host you are, you want *zero* slices left over. Sounds like a recipe for a mathematical migraine, right?
Wrong! The LCM is here to rescue us from pizza-planning paralysis! We need to find a number that *both* 25 and 45 divide into evenly. That number is our magical "everyone gets the same" slice count.
Listing the Multiples: The Slightly Slower Route
One way to find the LCM is by listing out the multiples of each number. It's like a mathematical staring contest to see which number shows up first on both lists. It might take longer, but it's as reliable as your grandma's apple pie recipe.
Let's start with 25. Here come the multiples: 25, 50, 75, 100, 125, 150, 175, 200, 225...
Now, 45 gets its turn: 45, 90, 135, 180, 225... Bam! Look what we found: 225 is the first number that appears on both lists.
So, the LCM of 25 and 45 is 225. It took us a while but we got there! That means you need to aim for a total of 225 slices to keep everyone happy and avoid leftover pizza sadness.
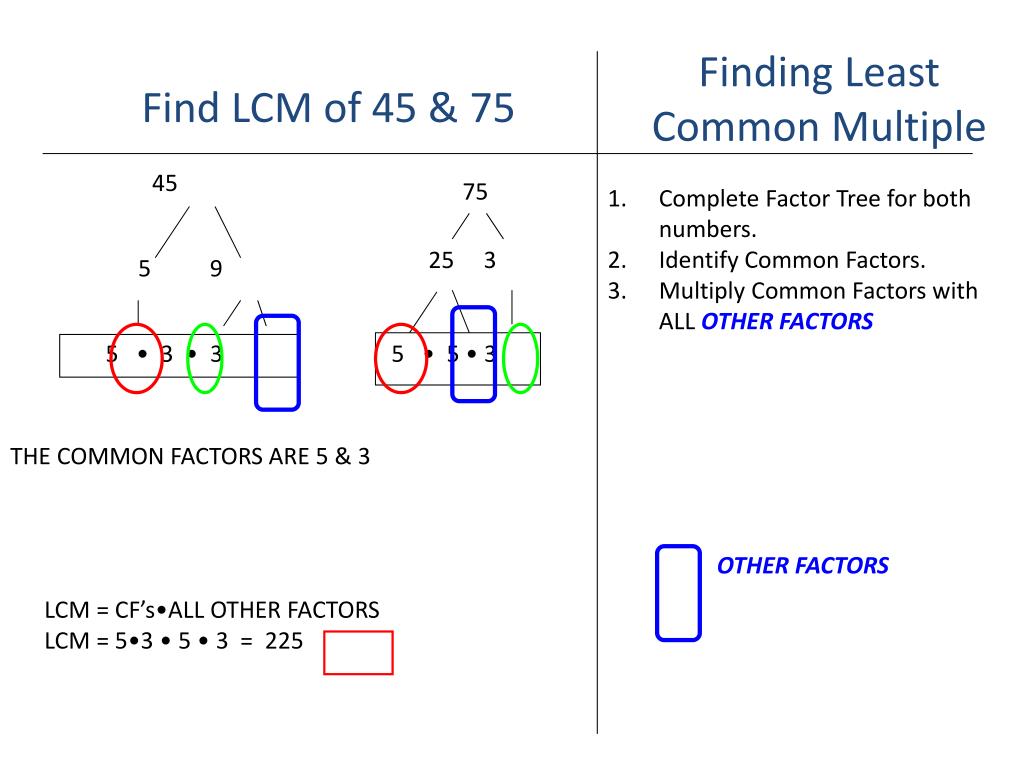
Prime Factorization: The Speedy Superhero Approach
Listing multiples works, but what if the numbers are HUGE? We need a superhero strategy! That's where prime factorization comes in. Don't let the name intimidate you; it's just breaking down numbers into their prime building blocks.
Think of prime numbers as the atoms of the number world – numbers that are only divisible by 1 and themselves (like 2, 3, 5, 7, 11, and so on). We are going to break 25 and 45 to smaller pieces.
First, let's factorize 25. What prime numbers multiply to give us 25? Well, 5 x 5 = 25. So, the prime factorization of 25 is 5². It’s just like 5 to the power of 2.
Next, let's tackle 45. We can break it down into 3 x 3 x 5 = 45. So, the prime factorization of 45 is 3² x 5.
Now for the magic trick! To find the LCM, we take the highest power of each prime factor that appears in either factorization.
We have the prime factors 3 and 5. The highest power of 3 is 3² (from the factorization of 45). The highest power of 5 is 5² (from the factorization of 25).
Therefore, the LCM is 3² x 5² = 9 x 25 = 225. BOOM! Same answer, but way faster! You are like a mathematical wizard!
So, back to your pizza party. How many of each pizza do you need to order? To get 225 slices, you'll need 225 / 25 = 9 of the larger pizzas (25 slices each) and 225 / 45 = 5 of the mini pizzas (45 slices each). Problem solved!
Beyond Pizza: Real-World LCM Adventures!
Okay, pizza parties are pretty epic, but the LCM is actually useful in all sorts of everyday situations. It's not just some abstract math concept lurking in textbooks.
Let’s say you are buying hot dogs and buns. Hot dogs come in packs of 25, and buns come in packs of 45. To avoid leftovers, you need to find the LCM of 25 and 45.
We already know it's 225, so you'd need to buy 9 packs of hot dogs and 5 packs of buns to have the same number of each. No more lonely hot dog or bun looking for its partner in culinary crime!
Scheduling Shenanigans: LCM to the Rescue!
Imagine you have two friends. One friend visits you every 25 days, and the other visits you every 45 days. You are trying to figure out when both will visit you at the same time.
Again, the LCM of 25 and 45 comes to the rescue. You will both meet after 225 days. Mark your calendar!
The LCM ensures everyone arrives at the same point at the same time, without any scheduling snafus. No more awkwardly staggered arrivals or missed connections!
LCM: The Unexpected Party Hero
So, there you have it! The Least Common Multiple, demystified and ready to be your mathematical sidekick. It might sound intimidating, but with a little practice, it's as easy as ordering a pizza (or nine!).
Whether you're planning a party, coordinating schedules, or just trying to avoid hot dog/bun loneliness, the LCM is a surprisingly powerful tool. Embrace it, and prepare to be amazed by its problem-solving prowess.
Now go forth and conquer those real-world challenges with your newfound LCM knowledge! And remember, math can be fun, especially when it involves pizza!