Alright, buckle up buttercups! We're diving into the thrilling world of… Modulus of Elasticity! I know, I know, it sounds like something only a super-powered science wizard would understand. But trust me, it's easier than parallel parking a unicycle (and WAY more useful!).
Think of it this way: imagine you're holding a rubber band. You stretch it, right? Some rubber bands stretch a lot with very little effort. Others are tougher, requiring you to put some muscle into it. That "toughness," that resistance to stretching, that, my friends, is related to the Modulus of Elasticity. We're going to find out how to measure it!
The Basic Idea: Poke It, Prod It, Measure It!
Okay, maybe don't *actually* poke anything with a sharp stick (unless you're a qualified scientist working in a lab, and even then, be careful!). The core idea is to apply a force to a material and see how much it deforms. We need three crucial ingredients:
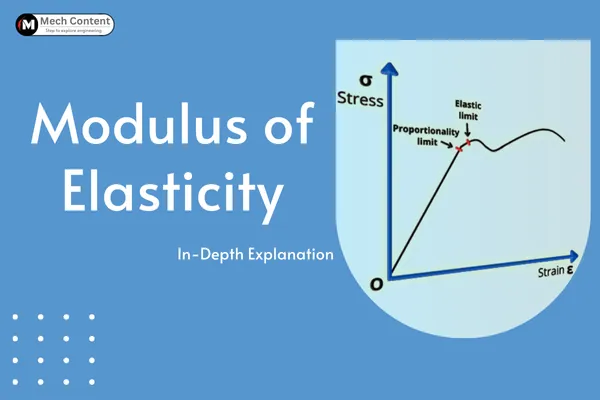
- Stress: This is the amount of force you're applying per unit area. Imagine standing on a yoga mat versus standing on a single stiletto heel. Same force (your weight), very different pressure! Stress is like that stiletto heel – it's concentrated force.
- Strain: This is how much the material deforms relative to its original size. If your rubber band was 10 cm long and you stretched it to 12 cm, the strain is the change in length (2 cm) divided by the original length (10 cm), giving you 0.2 (or 20%).
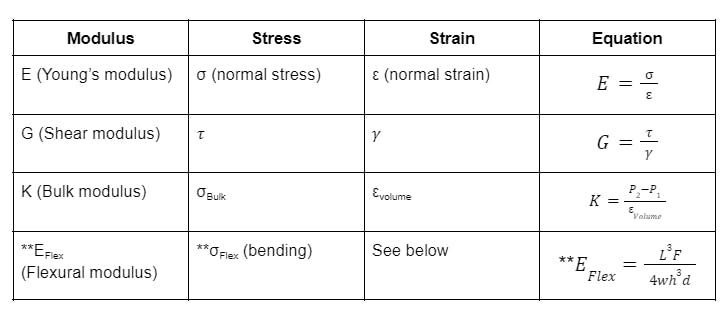
- Modulus of Elasticity (E): This is the star of our show! It's simply the ratio of stress to strain. Think of it like this: E = Stress / Strain. The higher the value of E, the stiffer the material.
Let's Get (Slightly) Mathy!
Don't run away screaming! The math is super simple, I promise! We'll break it down:
Step 1: Apply the Force (and Measure It!)
You'll need to apply a known force (F) to your material. This could be anything from hanging a weight to using a fancy machine that pushes or pulls. It all depends on what you have.
Step 2: Measure the Area (A Little Geometry Never Hurt Anyone!)
You need to know the cross-sectional area (A) of the material you're testing. If it's a wire, it's the area of a circle (πr²). If it's a rectangular beam, it's length times width. Dust off those geometry skills!
Step 3: Calculate the Stress (Stress = Force / Area)
This is where the magic happens! Divide the force (F) you applied by the cross-sectional area (A). That gives you the stress: Stress = F / A. The units are usually Pascals (Pa) or pounds per square inch (psi).
Step 4: Measure the Deformation (How Much Did It Change?)
Measure the original length of the material (L₀) before you applied any force. Then, measure the length (L) after you applied the force. The change in length is ΔL = L - L₀.
Step 5: Calculate the Strain (Strain = Change in Length / Original Length)
Divide the change in length (ΔL) by the original length (L₀). This gives you the strain: Strain = ΔL / L₀. Strain is usually a dimensionless number (no units).
Step 6: Calculate the Modulus of Elasticity (E = Stress / Strain)
Finally! Divide the stress (calculated in Step 3) by the strain (calculated in Step 5). This gives you the Modulus of Elasticity: E = Stress / Strain. The units for E are the same as the units for stress (usually Pascals or psi).
Example Time! Let's Bend a Spoon (Metaphorically, of Course!)
Okay, maybe don't *actually* bend a spoon. But imagine you have a titanium spoon (because why not?). Let's say you apply a force of 10 Newtons (N) to a small section of it. The cross-sectional area of that section is 0.00001 square meters (m²). The original length of that section is 0.01 meters (m), and it stretches by 0.000001 meters (m).
- Stress = 10 N / 0.00001 m² = 1,000,000 Pa
- Strain = 0.000001 m / 0.01 m = 0.0001
- E = 1,000,000 Pa / 0.0001 = 10,000,000,000 Pa (or 10 GPa!)
That's a big number! Titanium is pretty stiff. Now you know how to quantify it!
Important Considerations (Because Science!)
- Temperature: Temperature can affect the Modulus of Elasticity. Materials tend to get softer at higher temperatures.
- Type of Stress: We talked about tensile stress (stretching), but there's also compressive stress (squishing) and shear stress (twisting). Each type of stress can have a different Modulus of Elasticity.
- Material Properties: The Modulus of Elasticity is an intrinsic property of the material, but it can be affected by factors like impurities and manufacturing processes.
So, there you have it! You're now equipped to find the Modulus of Elasticity of… well, almost anything (within reason, and with appropriate safety precautions, of course!). Go forth and measure! You've earned it!